Équilatère — Une hyperbole est dite équilatère lorsque ses deux asymptotes sont perpendiculaires. Brianchon Poncelet Lorsqu un triangle est inscrit dans une hyperbole équilatère, son orthocentre est aussi sur l hyperbole. En fait, le centre du… … Wikipédia en Français
équilatère — (é kui la tê r ; ui prononcé comme dans huile) adj. Terme de géométrie. Synonyme peu usité d équilatéral. Il s applique surtout à l hyperbole dont le demi axe est égal à l ordonnée centrale rendue réelle. • L asymptote coupe par moitié les… … Dictionnaire de la Langue Française d'Émile Littré
ÉQUILATÈRE — adj. des deux genres T. de Géom. Il se dit D une figure dont les côtés sont égaux à ceux d une autre … Dictionnaire de l'Academie Francaise, 7eme edition (1835)
ÉQUILATÈRE — adj. des deux genres T. de Géométrie Dont les deux symptotes sont rectangulaires, en parlant d’une Hyperbole … Dictionnaire de l'Academie Francaise, 8eme edition (1935)
CONIQUES — L’étude des coniques a été pendant deux millénaires le terrain de prédilection des géomètres qui ont accumulé sur ce sujet d’innombrables théorèmes. Dès la fin du IIIe siècle avant J. C., les mathématiciens avaient obtenu par des méthodes… … Encyclopédie Universelle
hyperbole — [ ipɛrbɔl ] n. f. • yperbole XIIIe; lat. hyperbole, gr. huperbolê, de huper « au dessus » et ballein « lancer » I ♦ Rhét. Figure de style qui consiste à mettre en relief une idée au moyen d une expression qui la dépasse (opposé à litote). ⇒ … Encyclopédie Universelle
Conique — En mathématiques, et plus précisément en géométrie, les coniques constituent une famille très utilisée de courbes planes algébriques, qui peuvent être définies de plusieurs manières différentes, toutes équivalentes entre elles. Sommaire 1… … Wikipédia en Français
Hyperboloide — Hyperboloïde En mathématiques, un hyperboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s étendre à l infini. Les… … Wikipédia en Français
Hyperboloïde — En mathématiques, et plus précisément en géométrie, un hyperboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s étendre… … Wikipédia en Français
FONCTIONS ANALYTIQUES - Représentation conforme — La représentation conforme la plus anciennement connue est la projection stéréographique, inventée par les Grecs (Hipparque, Ptolémée). Les problèmes cartographiques conduisirent à la découverte d’autres applications conservant les angles d’un… … Encyclopédie Universelle
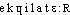]. Mais [eki-] ds PASSY 1914 et, à titre de var., ds BARBEAU-RODHE 1930. Cf. équi-. Le mot est admis ds Ac. 1762-1932. Étymol. et Hist. 1. XIIIe s. triangle equilatere « qui a tous ses côtés égaux » (Comput. f. 16 ds LITTRÉ); 2. 1755 hyperbole équilatère « dont les axes sont égaux, ses asymptotes étant perpendiculaires » (Encyclop.). Empr. au b. lat. aequilaterus (formé de aequi, v. équi- et de latus, lateris « côté ») « équilatéral ».équilatère [ekɥilatɛʀ] adj.ÉTYM. 1755; « qui a tous ses côtés égaux », XIIIe (→ Équilatéral); de équi-, et -latère.❖♦ Géom. || Hyperbole équilatère, à asymptotes perpendiculaires.